Topology of time series¶
This notebook explores how giotto-tda can be used to gain insights
from time-varying data by using ideas from from dynamical systems and
persistent homology.
If you are looking at a static version of this notebook and would like to run its contents, head over to GitHub and download the source.
Useful references¶
Topological Methods for the Analysis of Data by Jose Perea
The sliding window notebooks from Chris Tralie’s TDALabs
Detection of gravitational waves using topological data analysis and convolutional neural network: An improved approach by Christopher Bresten and Jae-Hun Jung. We thank Christopher Bresten for sharing the code and data used in the article.
See also¶
Gravitational waves detection, where,following arXiv:1910.08245, the Takens embedding technique is shown to be effective for the detection of gravitational waves signals buried in background noise.
Topology in time series forecasting, in which the Takens embedding technique is used in time series forecasting tasks by using sliding windows.
Topological feature extraction using VietorisRipsPersistence and PersistenceEntropy for a quick introduction to general topological feature extraction in
giotto-tda.
License: AGPLv3
From time series to time delay embeddings¶
The first step in analysing the topology of time series is to construct a time delay embedding or Takens embedding, named after Floris Takens who pioneered its use in the study of dynamical systems. A time delay embedding can be thought of as sliding a “window” of fixed size over a signal, with each window represented as a point in a (possibly) higher-dimensional space. A simple example is shown in the animation below, where pairs of points in a 1-dimensional signal are mapped to coordinates in a 2-dimensional embedding space.
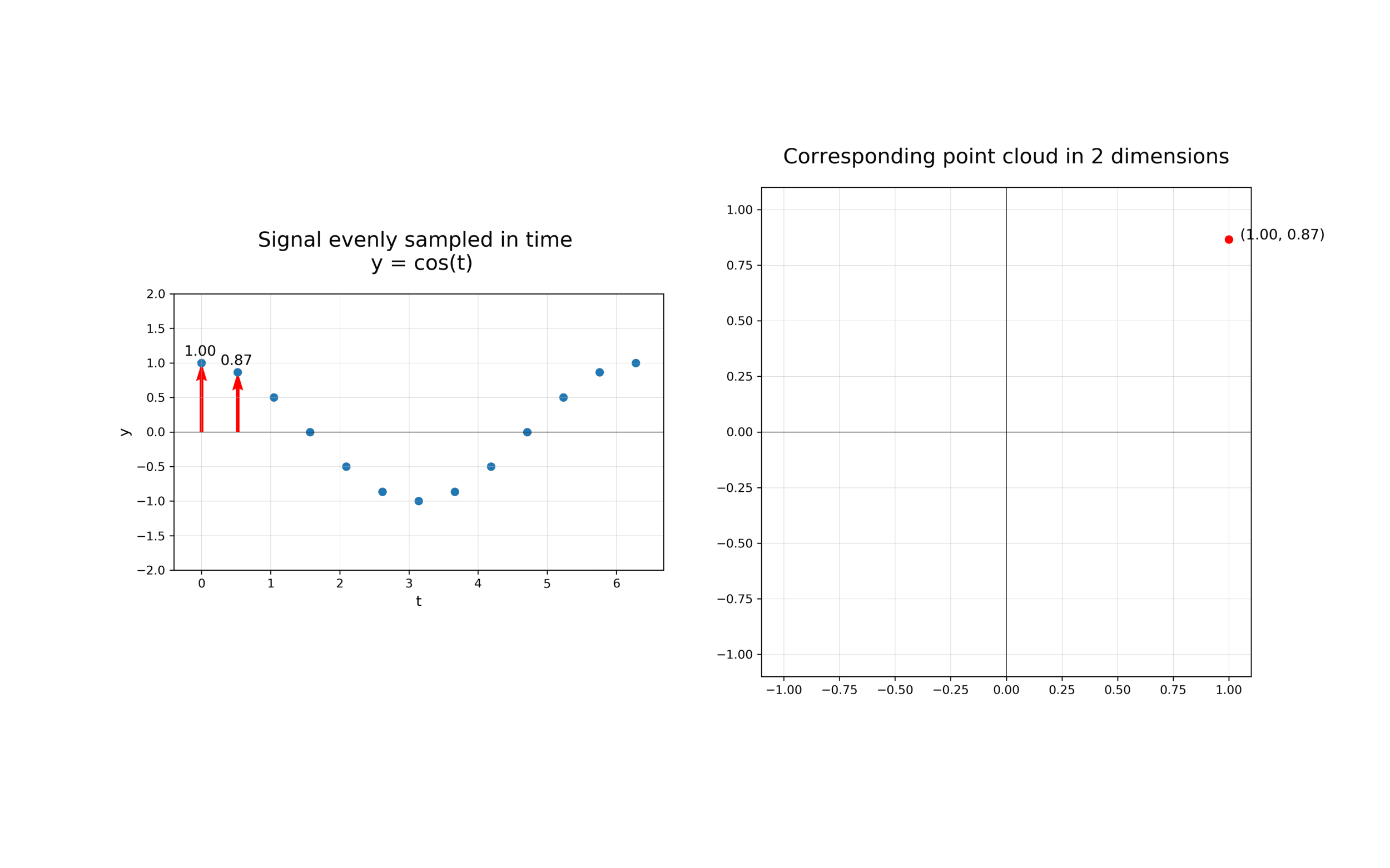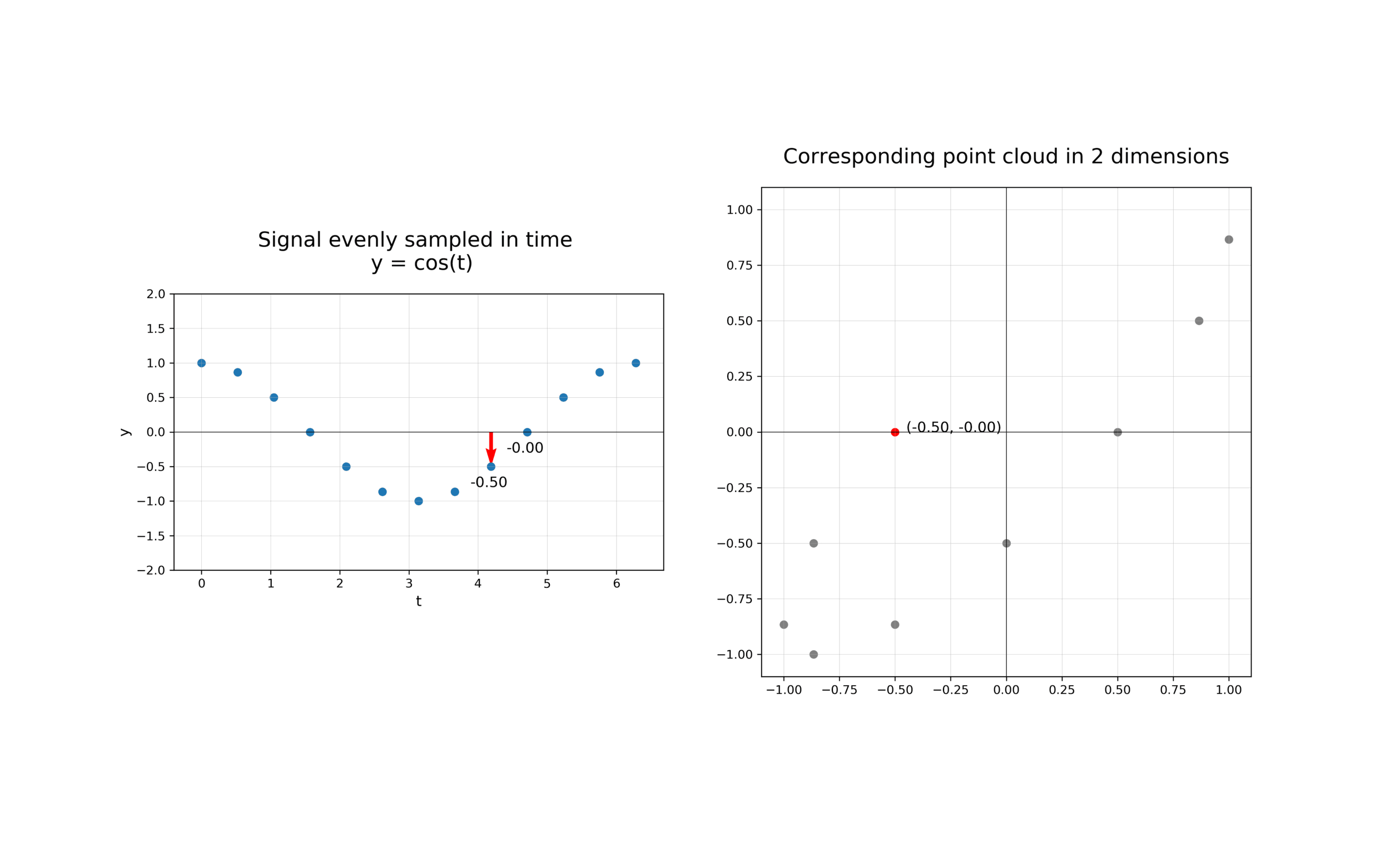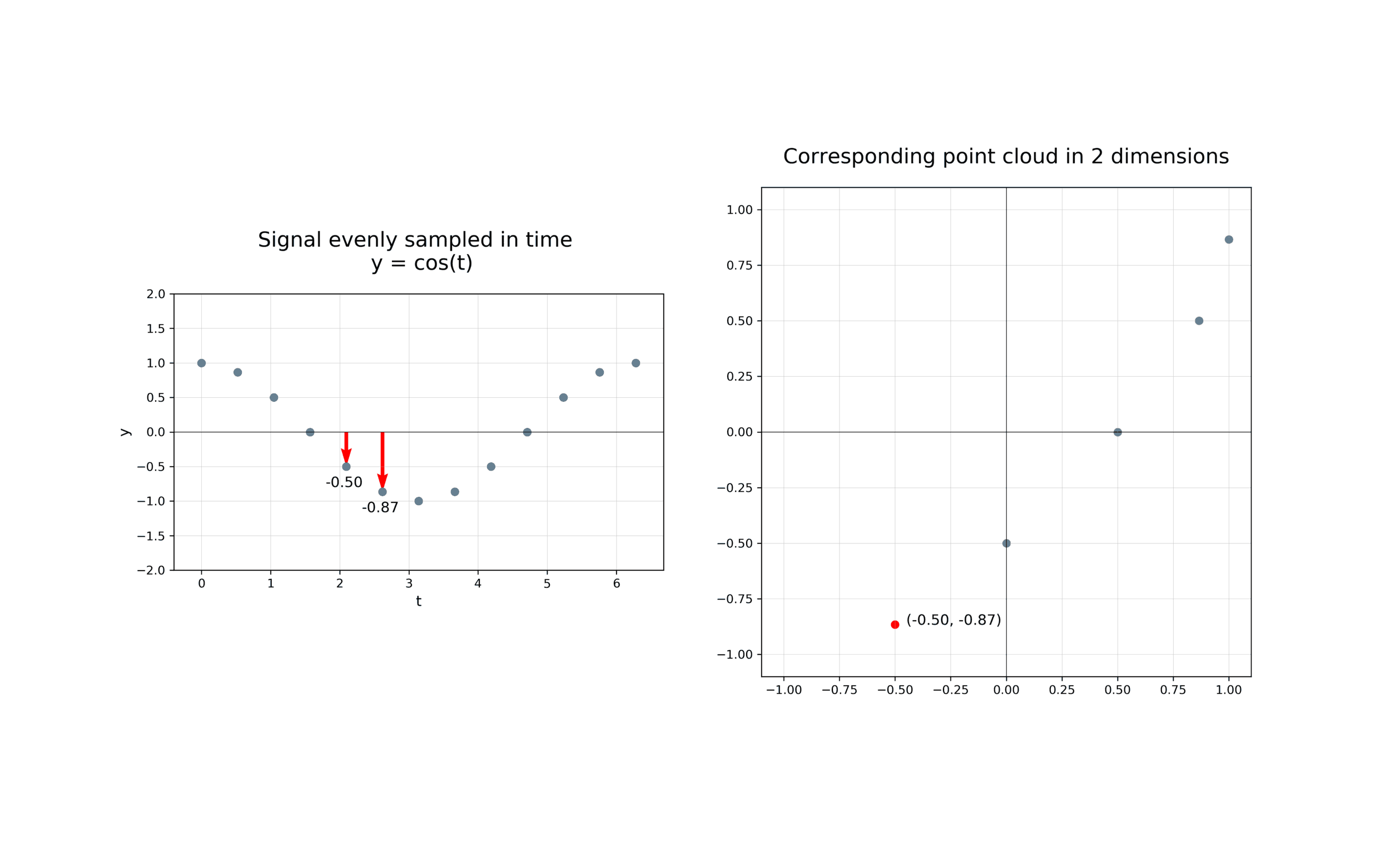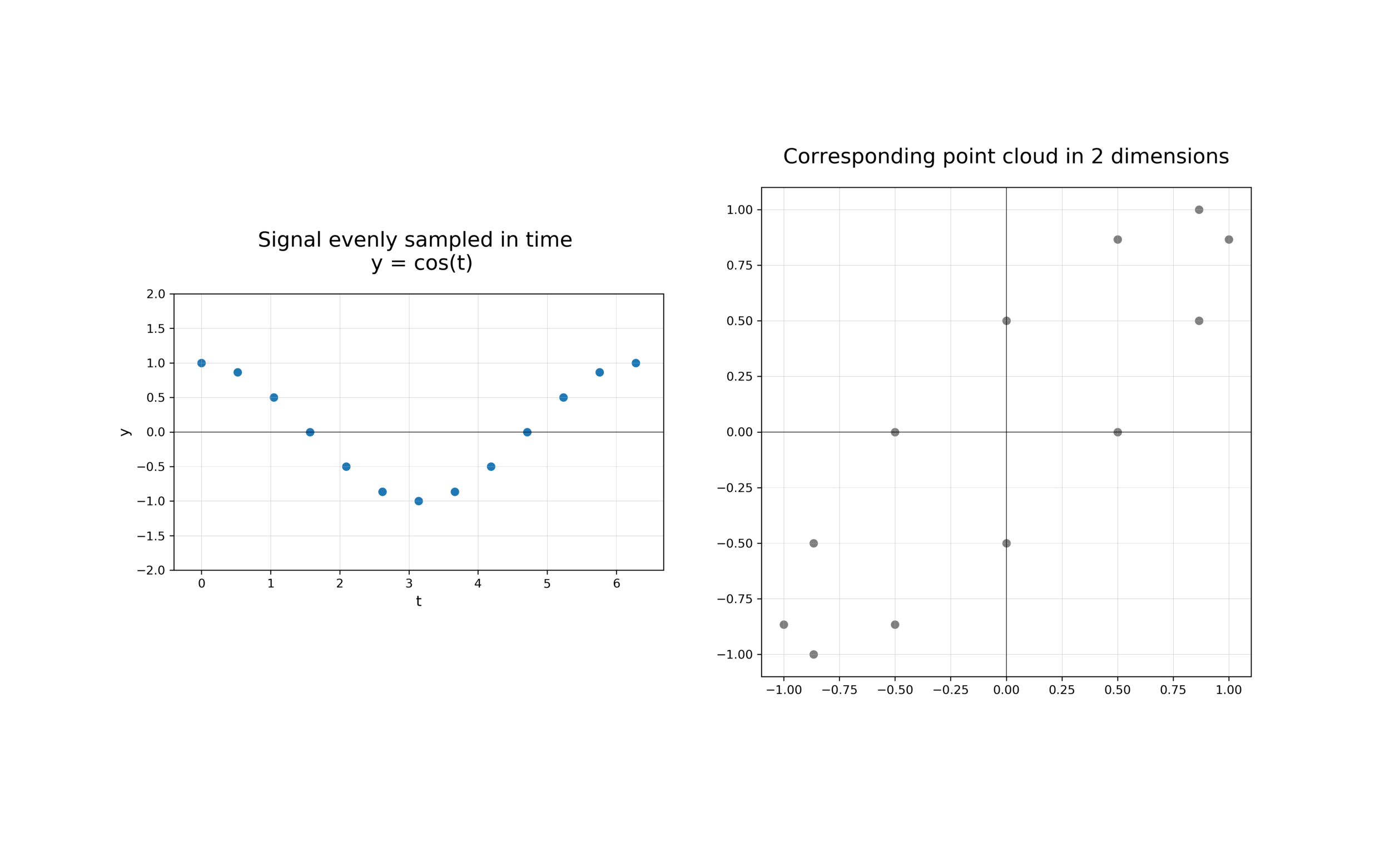
A 2-dimensional time delay embedding¶
More formally, given a time series \(f(t)\), one can extract a sequence of vectors of the form \(f_i = [f(t_i), f(t_i + \tau), f(t_i + 2 \tau), \ldots, f(t_i + (d-1) \tau)] \in \mathbb{R}^{d}\), where \(d\) is the embedding dimension and \(\tau\) is the time delay. The quantity \((d-1)\tau\) is known as the “window size” and the difference between \(t_{i+1}\) and \(t_i\) is called the stride. In other words, the time delay embedding of \(f\) with parameters \((d,\tau)\) is the function
and the main idea we will explore in this notebook is that if \(f\) has a non-trivial recurrent structure, then the image of \(TD_{d,\tau}f\) will have non-trivial topology for appropriate choices of \((d, \tau)\).
A periodic example¶
As a warm-up, recall that a function is periodic with period \(T > 0\) if \(f(t + T) = f(t)\) for all \(t \in \mathbb{R}\). For example, consider the function \(f(t) = \cos(5 t)\) which can be visualised as follows:
import numpy as np
import plotly.graph_objects as go
x_periodic = np.linspace(0, 10, 1000)
y_periodic = np.cos(5 * x_periodic)
fig = go.Figure(data=go.Scatter(x=x_periodic, y=y_periodic))
fig.update_layout(xaxis_title="Timestamp", yaxis_title="Amplitude")
fig.show()
We can show that periodicity implies ellipticity of the time delay
embedding. To do that we need to specify the embedding dimension
\(d\) and the time delay \(\tau\) for the Takens embedding,
which in giotto-tda can be achieved as follows:
from gtda.time_series import SingleTakensEmbedding
embedding_dimension_periodic = 3
embedding_time_delay_periodic = 8
stride = 10
embedder_periodic = SingleTakensEmbedding(
parameters_type="fixed",
n_jobs=2,
time_delay=embedding_time_delay_periodic,
dimension=embedding_dimension_periodic,
stride=stride,
)
Tip: You can use the stride parameter to downsample the time
delay embedding. This is handy when you want to quickly compute
persistence diagrams on a dense signal.
Let’s apply this embedding to our one-dimensional time series to get a 3-dimensional point cloud:
y_periodic_embedded = embedder_periodic.fit_transform(y_periodic)
print(f"Shape of embedded time series: {y_periodic_embedded.shape}")
Shape of embedded time series: (99, 3)
We can then use giotto-tda’s plotting API to visualise the result:
from gtda.plotting import plot_point_cloud
plot_point_cloud(y_periodic_embedded)
As promised, the periodicity of \(f\) is reflected in the ellipticity of the time delay embedding! It turns out that in general, periodic functions trace out ellipses in \(\mathbb{R}^{d}\).
A non-periodic example¶
Here is another type of recurrent behaviour: if we let \(f(t) = \cos(t) + \cos(\pi t)\) then it follows that \(f\) is not periodic since the ratio of the two frequencies is irrational, i.e. we say that \(\cos(t)\) and \(\cos(\pi t)\) are incommensurate. Nevertheless, their sum produces recurrent behaviour:
x_nonperiodic = np.linspace(0, 50, 1000)
y_nonperiodic = np.cos(x_nonperiodic) + np.cos(np.pi * x_nonperiodic)
fig = go.Figure(data=go.Scatter(x=x_nonperiodic, y=y_nonperiodic))
fig.update_layout(xaxis_title="Timestamp", yaxis_title="Amplitude")
fig.show()
As before, let’s create a time delay embedding for this signal and visualise the resulting point cloud:
embedding_dimension_nonperiodic = 3
embedding_time_delay_nonperiodic = 16
stride = 3
embedder_nonperiodic = SingleTakensEmbedding(
parameters_type="fixed",
n_jobs=2,
time_delay=embedding_time_delay_nonperiodic,
dimension=embedding_dimension_nonperiodic,
stride=stride,
)
y_nonperiodic_embedded = embedder_nonperiodic.fit_transform(y_nonperiodic)
plot_point_cloud(y_nonperiodic_embedded)
From time delay embeddings to persistence diagrams¶
In the examples above we saw that the resulting point clouds appear to
exhibit distinct topology. We can verify this explicitly using
persistent homology! First we need to reshape our point cloud arrays in
a form suitable for the VietorisRipsPersistence
transformer,
namely (n_samples, n_points, n_dimensions):
y_periodic_embedded = y_periodic_embedded[None, :, :]
y_nonperiodic_embedded = y_nonperiodic_embedded[None, :, :]
The next step is to calculate the persistence diagrams associated with
each point cloud. In giotto-tda we can do this with the
Vietoris-Rips construction as follows:
from gtda.homology import VietorisRipsPersistence
# 0 - connected components, 1 - loops, 2 - voids
homology_dimensions = [0, 1, 2]
periodic_persistence = VietorisRipsPersistence(
homology_dimensions=homology_dimensions, n_jobs=6
)
print("Persistence diagram for periodic signal")
periodic_persistence.fit_transform_plot(y_periodic_embedded)
nonperiodic_persistence = VietorisRipsPersistence(
homology_dimensions=homology_dimensions, n_jobs=6
)
print("Persistence diagram for nonperiodic signal")
nonperiodic_persistence.fit_transform_plot(y_nonperiodic_embedded);
Persistence diagram for periodic signal
Persistence diagram for nonperiodic signal
array([[[0. , 0.00669674, 0. ],
[0. , 0.00935366, 0. ],
[0. , 0.01807661, 0. ],
...,
[0.25856125, 0.26006246, 1. ],
[0.77751291, 1.70462596, 2. ],
[0.77221543, 1.73804259, 2. ]]])
What can we conclude from these diagrams? The first thing that stands out is the different types of homology dimensions that are most persistent. In the periodic case we see a single point associated with 1-dimensional persistent homology, namely a loop! On the other hand, the non-periodic signal has revealed two points associated with 2-dimensional persistent homology, namely voids. These clear differences in topology make the time delay embedding technique especially powerful at classifying different time series.
Picking the embedding dimension and time delay¶
In the examples above, we manually chose values for the embedding dimension \(d\) and time delay \(\tau\). However, it turns out there are two techniques that can be used to determine these parameters automatically:
Mutual information to determine \(\tau\)
False nearest neighbours to determine \(d\)
In giotto-tda, these techniques are applied when we select
parameters_type="search" in the SingleTakensEmbedding
transformer, e.g.
embedder = SingleTakensEmbedding(
parameters_type="search", time_delay=time_delay, dimension=embedding_dimension,
)
where the values of time_delay and embedding_dimension provide
upper bounds on the search algorithm. Before applying this to our
sample signals, let’s have a look at how these methods actually work
under the hood.
Mutual information¶
To determine an optimal value for \(\tau\) we first calculate the maximum \(x_\mathrm{max}\) and minimum \(x_\mathrm{min}\) values of the time series, and divide the interval \([x_\mathrm{min}, x_\mathrm{max}]\) into a large number of bins. We let \(p_k\) be the probability that an element of the time series is in the \(k\)th bin and let \(p_{j,k}\) be the probability that \(x_i\) is in the \(j\)th bin while \(x_{i+\tau}\) is in the \(k\)th bin. Then the mutual information is defined as:
The first minimum of \(I(\tau)\) gives the optimal time delay since there we get the most information by adding \(x_{i+\tau}\).
False nearest neighbours¶
The false nearest neighbours algorithm is based on the assumption that “unfolding” or embedding a deterministic system into successively higher dimensions is smooth. In other words, points which are close in one embedding dimension should be close in a higher one. More formally, if we have a point \(p_i\) and neighbour \(p_j\), we check if the normalised distance \(R_i\) for the next dimension is greater than some threshold \(R_\mathrm{th}\):
If \(R_i > R_\mathrm{th}\) then we have a “false nearest neighbour” and the optimal embedding dimension is obtained by minimising the total number of such neighbours.
Running the search algorithm¶
Let’s now apply these ideas to our original signals to see what the algorithm determines as optimal choices for \(d\) and \(\tau\). We will allow the search to scan up to relatively large values of \((d, \tau)\) to ensure we do not get stuck in a sub-optimal minimum.
For the periodic signal, we initialise the Takens embedding as follows:
max_embedding_dimension = 30
max_time_delay = 30
stride = 5
embedder_periodic = SingleTakensEmbedding(
parameters_type="search",
time_delay=max_time_delay,
dimension=max_embedding_dimension,
stride=stride,
)
Let’s create a helper function to view the optimal values found during the search:
def fit_embedder(embedder: SingleTakensEmbedding, y: np.ndarray, verbose: bool=True) -> np.ndarray:
"""Fits a Takens embedder and displays optimal search parameters."""
y_embedded = embedder.fit_transform(y)
if verbose:
print(f"Shape of embedded time series: {y_embedded.shape}")
print(
f"Optimal embedding dimension is {embedder.dimension_} and time delay is {embedder.time_delay_}"
)
return y_embedded
y_periodic_embedded = fit_embedder(embedder_periodic, y_periodic)
Shape of embedded time series: (171, 6)
Optimal embedding dimension is 6 and time delay is 29
Although the resulting embedding is in a high dimensional space, we can apply dimensionality reduction techniques like principal component analysis to project down to 3-dimensions for visualisation:
from sklearn.decomposition import PCA
pca = PCA(n_components=3)
y_periodic_embedded_pca = pca.fit_transform(y_periodic_embedded)
plot_point_cloud(y_periodic_embedded_pca)
Now for the non-periodic case we have:
embedder_nonperiodic = SingleTakensEmbedding(
parameters_type="search",
n_jobs=2,
time_delay=max_time_delay,
dimension=max_embedding_dimension,
stride=stride,
)
y_nonperiodic_embedded = fit_embedder(embedder_nonperiodic, y_nonperiodic)
Shape of embedded time series: (186, 6)
Optimal embedding dimension is 6 and time delay is 14
pca = PCA(n_components=3)
y_nonperiodic_embedded_pca = pca.fit_transform(y_nonperiodic_embedded)
plot_point_cloud(y_nonperiodic_embedded_pca)
So we have embedding point clouds whose geometry looks clearly distinct;
how about the persistence diagrams? As we did earlier, we first need to
reshape our arrays into the form
(n_samples, n_points, n_dimensions):
y_periodic_embedded = y_periodic_embedded[None, :, :]
y_nonperiodic_embedded = y_nonperiodic_embedded[None, :, :]
The next step is to calculate the persistence diagrams associated with each point cloud:
homology_dimensions = [0, 1, 2]
periodic_persistence = VietorisRipsPersistence(homology_dimensions=homology_dimensions)
print("Persistence diagram for periodic signal")
periodic_persistence.fit_transform_plot(y_periodic_embedded)
nonperiodic_persistence = VietorisRipsPersistence(
homology_dimensions=homology_dimensions, n_jobs=6
)
print("Persistence diagram for nonperiodic signal")
nonperiodic_persistence.fit_transform_plot(y_nonperiodic_embedded);
Persistence diagram for periodic signal
Persistence diagram for nonperiodic signal
array([[[0. , 0.21571922, 0. ],
[0. , 0.23723184, 0. ],
[0. , 0.24294184, 0. ],
...,
[2.90700364, 3.02274561, 2. ],
[2.90693903, 3.06664085, 2. ],
[1.51555121, 3.0755682 , 2. ]]])
In this case the persistence diagram for the periodic signal is essentially unchanged, but the non-periodic signal now reveals two \(H_1\) points and one \(H_2\) one - the signature of a hypertorus! It turns out that in general, the image of \(TD_{d,\tau}f\) is a hypertorus.