Classifying 3D shapes

Techniques for analyzing 3D shapes are becoming increasingly important due to the vast number of sensors such as LiDAR that are capturing 3D data, as well as numerous computer graphics applications. These raw data are typically collected in the form of a point cloud, which corresponds to a set of 3D points \(\{p_i | i = 1, \ldots, n\}\), where each point \(p_i\) is a vector of its \((x, y, z)\) coordinates plus extra feature channels such as color, intensity etc. Typically, Euclidean distance is used to calculate the distances between any two points.

By finding suitable representations of these point clouds, machine learning can be used to solve a variety of tasks such as those shown in the figure below.

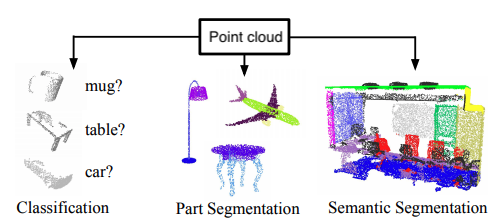
Figure reference: adapted from arxiv.org/abs/1612.00593.

This notebook examines how giotto-tda can be used to extract topological features from point cloud data and fed to a simple classifier to distinguish 3D shapes.

If you are looking at a static version of this notebook and would like to run its contents, head over to GitHub and download the source.

License: AGPLv3

Generate simple shapes

To get started, let’s generate a synthetic dataset of 10 noisy circles, spheres, and tori, where the effect of noise is to displace the points that sample the surfaces by a random amount in a random direction:

from data.generate_datasets import make_point_clouds

point_clouds_basic, labels_basic = make_point_clouds(n_samples_per_shape=10, n_points=20, noise=0.5)
point_clouds_basic.shape, labels_basic.shape

((30, 400, 3), (30,))

Here the labels are defined to that a circle is 0, a sphere is 1, and a torus is 2. Each point cloud corresponds to a sampling of the continuous surface – in this case 400 points are sampled per shape. As a sanity check, let’s visualise these points clouds using giotto-tda’s plotting API:

from gtda.plotting import plot_point_cloud

plot_point_cloud(point_clouds_basic[0])

plot_point_cloud(point_clouds_basic[10])

plot_point_cloud(point_clouds_basic[-1])

From data to persistence diagrams

In raw form, point cloud data is not well suited for most machine learning algorithms because we ultimately need a feature matrix \(X\) where each row corresponds to a single sample (i.e. point cloud) and each column corresponds to a particular feature. In our example, each point cloud corresponds to a collection of 3-dimensional vectors, so we need some way of representing this information in terms of a single vector \(x^{(i)}\) of feature values.

In this notebook we will use persistent homology to generate a topological summary of a point cloud in the form of a so-called persistence diagram. Perhaps the simplest way to understand persistent homology is in terms of growing balls around each point. The basic idea is that by keeping track of when the balls intersect we can quantify when topological features like connected components and loops are “born” or “die”.

For example, consider two noisy clusters and track their connectivity or “0-dimensional persistent homology” as we increase the radius of the balls around each point:

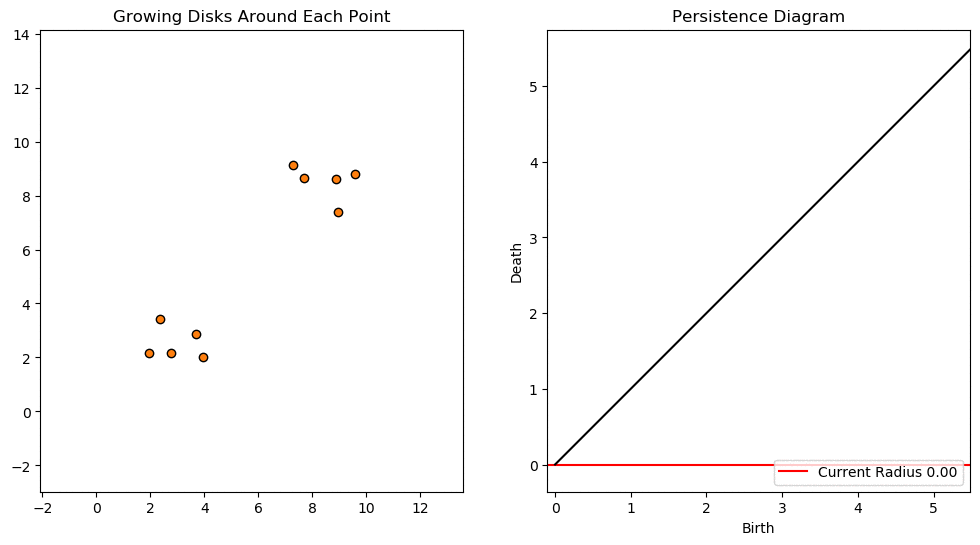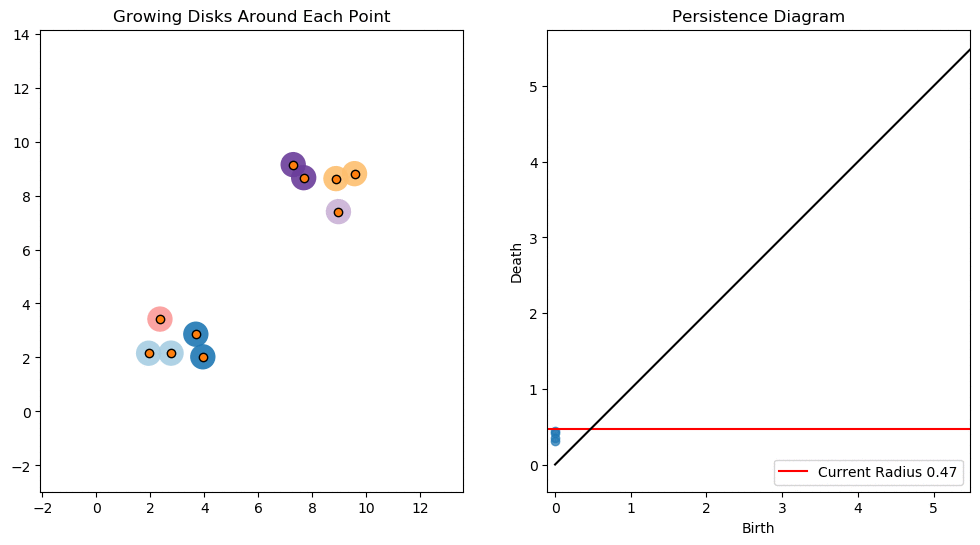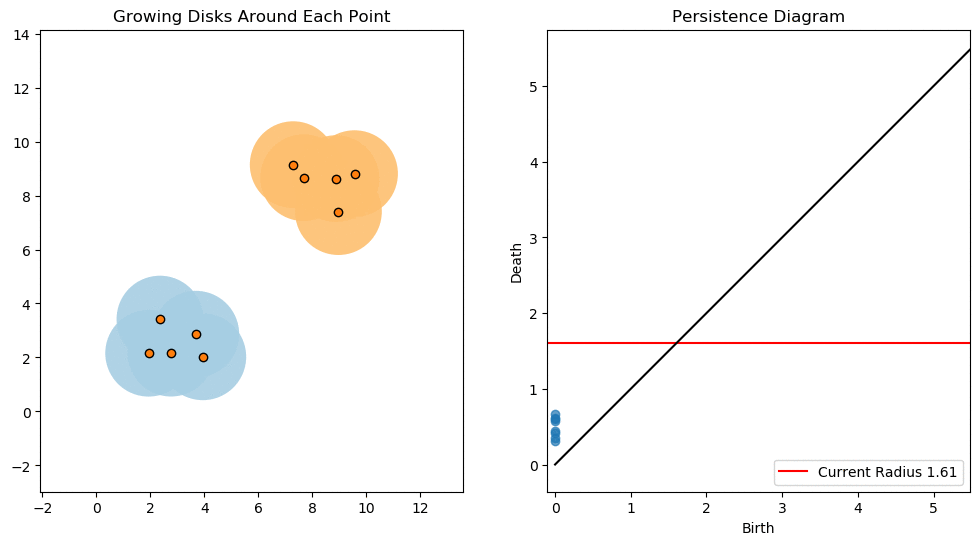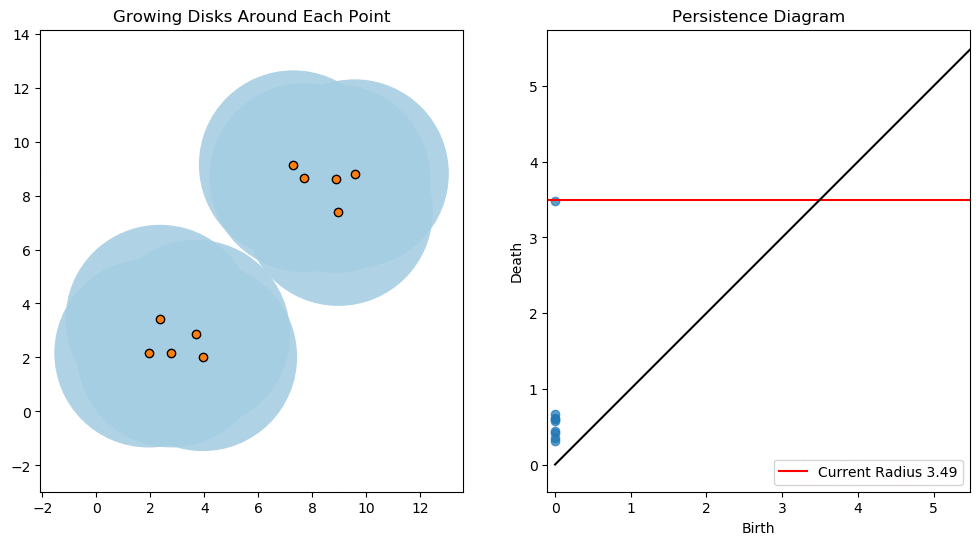
Figure reference: towardsdatascience.com/persistent-homology-with-examples-1974d4b9c3d0.

As the ball radius is grown from 0 to infinity, 0-dimensional persistent homology records when the ball in one connected component first intersects a ball of a different connected component (denoted by a different colour in the animation). At radius 0, a connected component for each point is born and once any two balls touch we have a death of a connected component with one color persisting and the other color vanishing. The vanishing of a color corresponds to a death, and therefore another point being added to the persistence diagram.

Behind the scenes, this process generating a persistence diagram from data involves several steps:

1. Construct a simplicial complex

The effect of connecting points as we increase some radius \(\epsilon\) results in the creation of geometric objects called simplices.

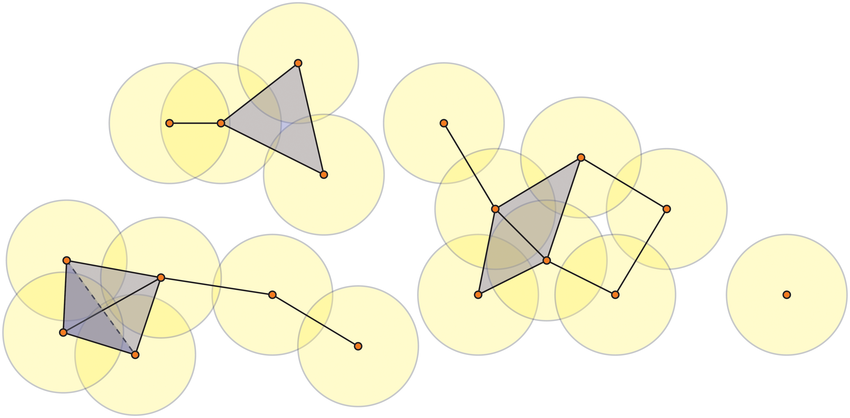
Figure reference: bit.ly/2z9yP1d.

A \(k\)-simplex \([p_0,\ldots,p_k]\) is the convex hull of a set of \(k+1\) affinely independent points in \(\mathbb{R}^n\). For example the 0-simplex is a point, the 1-simplex is a line, the 2-simplex is a triangular disc, and a 3-simplex a regular tetrahedron:

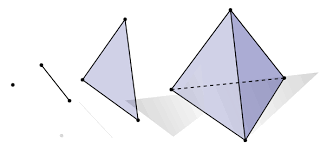
Figure reference: bit.ly/2X8AsUX.

Linking simplices together results in a simplicial complex \(X\), which for computational efficiency is often represented abstractly as finite subsets of the vertex set of \(X\). For example, the 2-complex shown below can be written as the set

\[X=\{a,b,c,d,e,[a,b],[b,c],[c,d],[d,e],[e,a],[b,e],[a,b,e]\}\,.\]

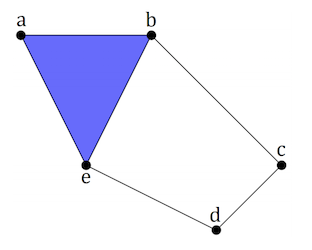
Figure reference: arxiv.org/abs/1904.11044.

One of the most common simplicial complexes one encounters in topological data analysis is the Vietoris-Rips complex, which is defined as the set of simplices \([p_0,\ldots,p_k]\) such that the distance metric \(d(p_i,p_j) \leq \epsilon\) for all \(i,j\).

2. Compute Betti numbers

Once the simplicial complex is constructed, we can ask questions about its topology. In particular, we can identify the presence of topological invariants such as connected pieces, holes and voids. This is achieved by computing quantities known as Betti numbers which are informally defined as follows:

The \(k\)th Betti number refers to the number of \(k\)-dimensional holes on a topological surface. The first few Betti numbers have the following definitions for 0-dimensional, 1-dimensional, and 2-dimensional simplicial complexes:

• \(b_0\) is the number of connected components,

• \(b_1\) is the number of one-dimensional or “circular” holes,

• \(b_2\) is the number of two-dimensional “voids” or “cavities”.

By computing Betti numbers of a range of scale values \(\epsilon\), we can track which topological features persist over this range. We can represent these changes in topology (technically homology) in terms of a persistence diagram, where each point corresponds to (birth, death) pairs, and points which are furthest away from the birth = death line correspond to the most persistent features.

Note: the reason we are talking about homology is because the \(n\)th Betti number represents the rank of the \(n\)th homology group \(H_n\).

An example showing the birth and death of “loops” (technically the homology group \(H_1\)) is shown below.

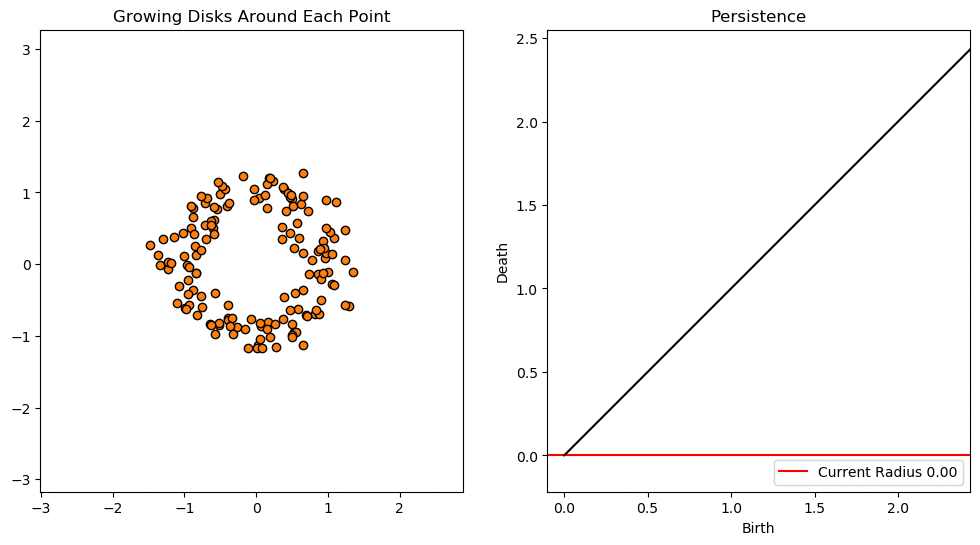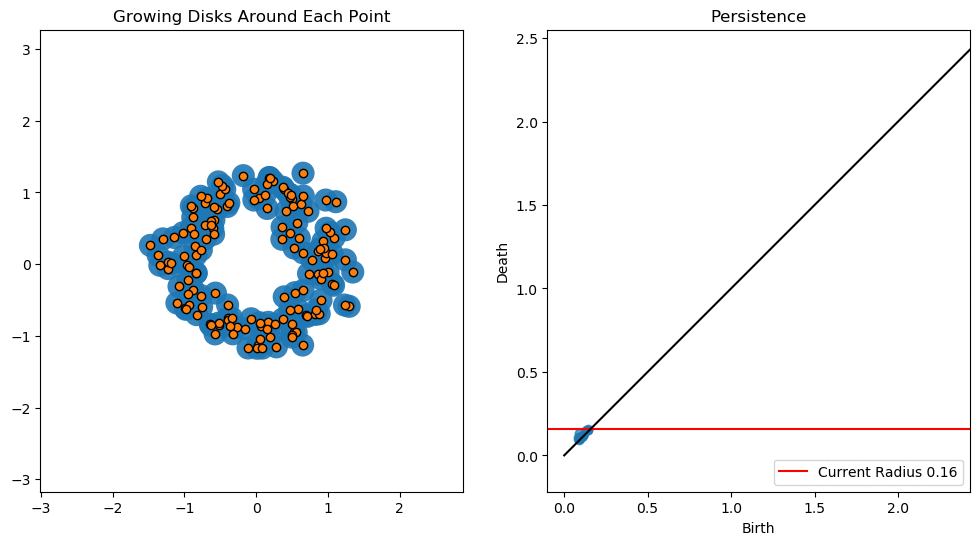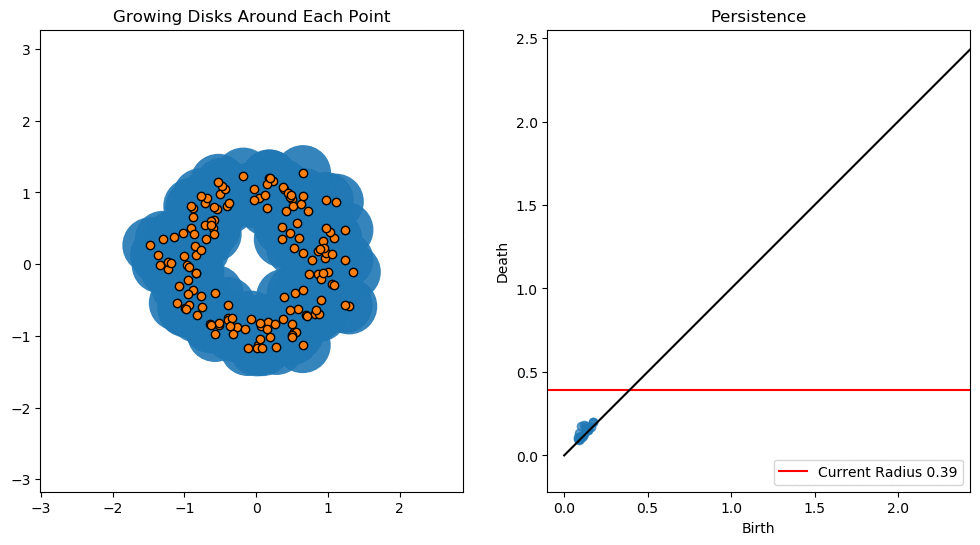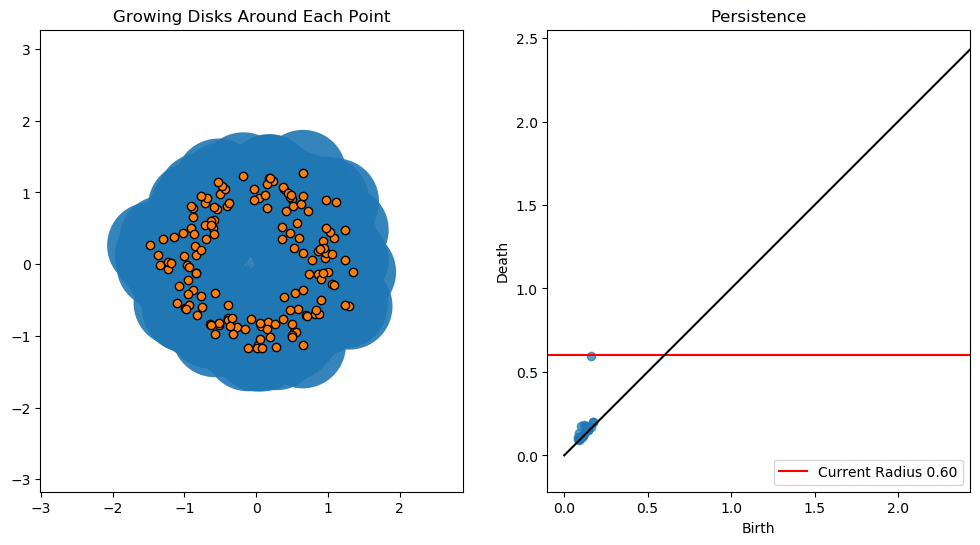
Figure reference: towardsdatascience.com/persistent-homology-with-examples-1974d4b9c3d0.

Let’s descend from abstraction and apply these concepts to our shape classification problem! In giotto-tda we can derive persistence diagrams from data by selecting the desired transformer in gtda.homology and instantiating the class just like a scikit-learn estimator. Once the transformer is instantiated, we can make use of the fit-transform paradigm to generate the diagrams:

from gtda.homology import VietorisRipsPersistence

# Track connected components, loops, and voids
homology_dimensions = [0, 1, 2]

# Collapse edges to speed up H2 persistence calculation!
persistence = VietorisRipsPersistence(
    metric="euclidean",
    homology_dimensions=homology_dimensions,
    n_jobs=6,
    collapse_edges=True,
)

diagrams_basic = persistence.fit_transform(point_clouds_basic)

Tip: in our example each point cloud has the same number of points so can be fed as single NumPy array. If you have varying number of points per point cloud, you can pass a list of arrays instead.

Once we have computed our persistence diagrams, we can compare how the circle, sphere and torus produce different patterns at each homology dimension:

from gtda.plotting import plot_diagram

# Circle
plot_diagram(diagrams_basic[0])

# Sphere
plot_diagram(diagrams_basic[10])

# Torus
plot_diagram(diagrams_basic[-1])

From the persistence diagrams we can see which persistent generators \(H_{1,2,3}\) are most persistent for each shape. In particular, we see that:

• the circle has one persistent generator \(H_1\) corresponding to a loop,

• the sphere has one persistent generator \(H_2\) corresponding to a void,

• the torus has three persistent generators, two for \(H_1\) and one for \(H_2\).

Although persistence diagrams are useful descriptors of the data, they cannot be used directly for machine learning applications. This is because different persistence diagrams may have different numbers of points, and basic operations like the addition and multiplication of diagrams are not well-defined.

To overcome these limitations, a variety of proposals have been made to “vectorize” persistence diagrams via embeddings or kernels which are well-suited for machine learning. In giotto-tda, we provide access to the most common vectorizations via the gtda.diagrams module.

For example, one such feature is known as persistence entropy which measures the entropy of points in a diagram \(D = \{(b_i, d_i)\}_{i\in I}\) according to

\[E(D) = - \sum_{i\in I} p_i \log p_i\]

where \(p_i =(d_i - b_i)/L_D\) and \(L_D = \sum_i (d_i - b_i)\). As we did for the persistence diagram calculation, we can use a transformer to calculate the persistent entropy associated with each homology generator \(H_{0,1,2}\):

from gtda.diagrams import PersistenceEntropy

persistence_entropy = PersistenceEntropy()

# calculate topological feature matrix
X_basic = persistence_entropy.fit_transform(diagrams_basic)

# expect shape - (n_point_clouds, n_homology_dims)
X_basic.shape

(30, 3)

Nice - we have found a way to represent each point cloud in terms of just three numbers! Note that this does not depend on the number of points in the original point cloud, although calculating the \(H_2\) generators becomes time consuming for point clouds of \(O(10^3)\) points (at least on a standard laptop).

By visualising the feature matrix

plot_point_cloud(X_basic)

we see that there are three distinct clusters, suggesting that a classifier should have no trouble finding a clean decision boundary!

Train a classifier

With our topological features at hand, the last step is to train a classifier. Since our dataset is small, we will use a Random Forest and make use of the OOB score to simulate accuracy on a validation set:

from sklearn.ensemble import RandomForestClassifier

rf = RandomForestClassifier(oob_score=True)
rf.fit(X_basic, labels_basic)

print(f"OOB score: {rf.oob_score_:.3f}")

OOB score: 1.000

Unsurprisingly, our classifier has perfectly separated the 3 classes. Next let’s try to combine all the steps as a single pipeline!

Putting it all together

Evidently, there are several data transformation steps that need to be executed in the right order to go from point clouds to predictions. Fortunately giotto-tda provides a Pipeline class to collect such sequences of transformations. Below is a small pipeline that reproduces all our steps:

from gtda.pipeline import Pipeline

steps = [
    ("persistence", VietorisRipsPersistence(metric="euclidean", homology_dimensions=homology_dimensions, n_jobs=6)),
    ("entropy", PersistenceEntropy()),
    ("model", RandomForestClassifier(oob_score=True)),
]

pipeline = Pipeline(steps)

By calling the fit method, the pipeline calls fit_transform on all transformers before calling fit on the final estimator:

pipeline.fit(point_clouds_basic, labels_basic)

Pipeline(steps=[('persistence',
                 VietorisRipsPersistence(homology_dimensions=[0, 1, 2],
                                         n_jobs=6)),
                ('entropy', PersistenceEntropy()),
                ('model', RandomForestClassifier(oob_score=True))])

We can then access the Random Forest model by its model key to pick out the OOB score:

pipeline["model"].oob_score_

1.0

A more realistic example

In the above example, the shapes were sufficiently distinct that it was easy to classify them according to their topological features. Here we consider a slightly more realistic example using point clouds from a variety of real-world objects. We will use the 3D dataset from Princeton’s COS 429 Computer Vision course. The dataset consists of 200 models organised into 20 classes of 10 objects each. We’ll use a subset consisting of a human, vase, dining_chair, and biplane:

from openml.datasets.functions import get_dataset

df = get_dataset('shapes').get_data(dataset_format='dataframe')[0]
df.head()

	x	y	z	target
0	0.341007	0.318606	0.096725	human_arms_out9
1	0.329226	0.421601	0.056749	human_arms_out9
2	0.446869	0.648674	0.124090	human_arms_out9
3	0.314729	0.217860	0.070847	human_arms_out9
4	0.426678	0.919195	0.047609	human_arms_out9

As a sanity check, let’s filter our pandas.DataFrame for a single member of a class, e.g. a biplane:

plot_point_cloud(df.query('target == "biplane0"')[["x", "y", "z"]].values)

Next, let’s collect all these point clouds in a single NumPy array:

import numpy as np

point_clouds = np.asarray(
    [
        df.query("target == @shape")[["x", "y", "z"]].values
        for shape in df["target"].unique()
    ]
)
point_clouds.shape

(40, 400, 3)

As we did with the simple shapes, we can calculate persistence diagrams for each of these point clouds:

persistence = VietorisRipsPersistence(
    metric="euclidean",
    homology_dimensions=homology_dimensions,
    n_jobs=6,
    collapse_edges=True,
)
persistence_diagrams = persistence.fit_transform(point_clouds)

By zooming in on the resulting diagrams, we can spot some persistent generators, but with far less signal than before:

# Index - (human_arms_out, 0), (vase, 10), (dining_chair, 20), (biplane, 30)
index = 30
plot_diagram(persistence_diagrams[index])

Next we convert each diagram into a 3-dimensional vector using persistent entropy and plot the resulting feature matrix:

persistence_entropy = PersistenceEntropy(normalize=True)
# Calculate topological feature matrix
X = persistence_entropy.fit_transform(persistence_diagrams)
# Visualise feature matrix
plot_point_cloud(X)

Unlike our simple shapes example, we do not see distinct clusters so we expect our classifier performance to be less than perfect in this case. Before we can train a model, we need to define a target vector for each point cloud. A crude, but simple way is to label each class with an integer starting from 0 to \(n_\mathrm{classes} - 1\):

labels = np.zeros(40)
labels[10:20] = 1
labels[20:30] = 2
labels[30:] = 3

rf = RandomForestClassifier(oob_score=True, random_state=42)
rf.fit(X, labels)
rf.oob_score_

0.6

Improving our model

In the analysis above we used persistence entropy to generate 3 topological features per persistence diagram (one per homology dimension). However, this choice of vectorisation is by no means unique, and in practice one can augment this information with other topological features to produce better models.

For example, a simple feature to include is the number of off-diagonal points per homology dimension:

from gtda.diagrams import NumberOfPoints

# Reshape single diagram to (n_samples, n_features, 3) format
diagram = persistence_diagrams[0][None, :, :]
# Get number of points for (H0, H1, H2)
NumberOfPoints().fit_transform(diagram)

array([[399,  87,  10]])

A more sophisticated feature is to calculate a vector of amplitudes for each persistence diagram. Here the main idea is to partition a diagram into subdiagrams (one per homology dimension) and use a metric to calculate the amplitude of each subdiagram relative to the trivial diagram (i.e. the one with points on the main diagonal). The result is a vector \(\boldsymbol{a} = (a_{q_1}, \ldots, a_{q_n})\), where the \(q_i\) range over the specified homology dimensions.

For example, we can calculate the Wasserstein amplitudes for a single diagram as follows:

from gtda.diagrams import Amplitude

Amplitude(metric='wasserstein').fit_transform(diagram)

array([[0.22923933, 0.06502641, 0.02047913]])

So now that we know how to generate new topological features, let’s combine them using scikit-learn’s utility function for feature unions:

from sklearn.pipeline import make_union

# Select a variety of metrics to calculate amplitudes
metrics = [
    {"metric": metric}
    for metric in ["bottleneck", "wasserstein", "landscape", "persistence_image"]
]

# Concatenate to generate 3 + 3 + (4 x 3) = 18 topological features
feature_union = make_union(
    PersistenceEntropy(normalize=True),
    NumberOfPoints(n_jobs=-1),
    *[Amplitude(**metric, n_jobs=-1) for metric in metrics]
)

The final step is to combine our feature extraction step with a classifier, fit the pipeline, and extract the OOB score:

pipe = Pipeline(
    [
        ("features", feature_union),
        ("rf", RandomForestClassifier(oob_score=True, random_state=42)),
    ]
)
pipe.fit(persistence_diagrams, labels)
pipe["rf"].oob_score_

0.825

By creating additional features, we’ve managed to improve our baseline model by about 30% – not bad!